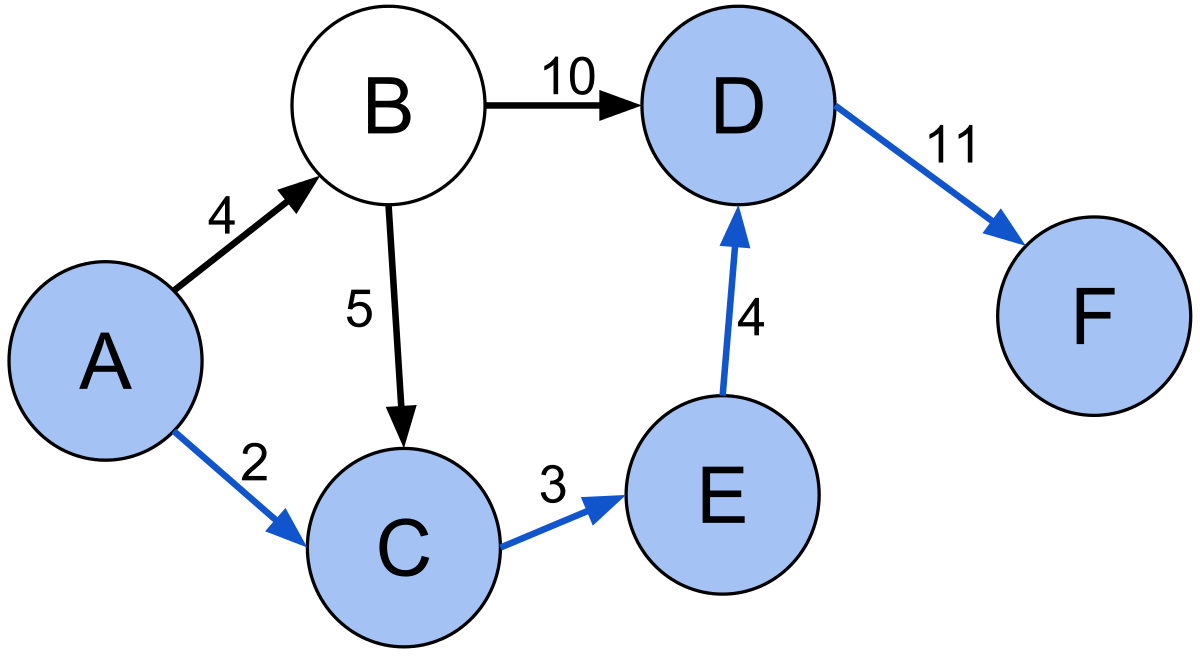
Finding Shortest Path Using Warshall’s Algorithm in C++
What is Adjacency Matrix?
An adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In adjacency matrix row means where the edge from and column means where the edge end. If there is value 0 in column – 3 and row – 2 that means there is no edge from node – 2 to node – 3.
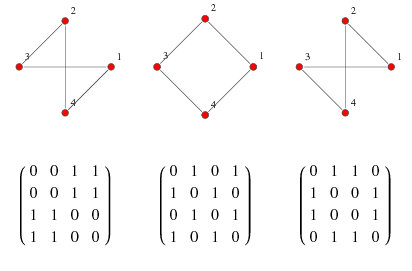
Difference Between Adjacency Matrix & Path Matrix
Key difference between Adjacency Matrix and Path Matrix is that an adjacency matrix is about direct edge where a path matrix is about whether can be traveled or not. Path matrix include both direct and indirect edges.
What is Shortest Path?
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.
A vertices can travel another vertices through many path. But the length of all path is not equal. A path which have the smallest length is called the shortest path.
What is Warshall Algorithm
Warshall Algorithm also known as Floyd-Warshall algorithm is used to find all pair shortest path problem from a given weighted graph. As a result of this algorithm, it will generate a matrix, which will represent the minimum distance from any node to all other nodes in the graph.
Shortest Path Using Warshall Algorithm in C++
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
//Function MIN to find minimum value between two value
long MIN(long a,long b){
if(a<b)return a;
else return b;
}
int main(){ //Main Function
int m,i,j,k;
//m is Number of Vertices or Point
//i,j,k is normal integer to forward loop
cout<<"Number of Vertics will be: ";
cin>>m;
long W[m][m],Q0[m][m],INF=1000000000;
//W is name of Adjacency Matrix which will take input the edges
//Q0 is the equivalent Matrix of W
//INF is a large number which works as infinity
//For loop to take input the Adjacency Matrix of weight of edges
cout<<"Enter the Weights Below in Adjacency Matrix Format in "<<m<<"x"<<m<<" size:"<<endl;
for(i=0;i<m;i++){
for(j=0;j<m;j++){
cin>>W[i][j];
}
}
cout<<endl;
//Finding Q0
for(i=0;i<m;i++){
for(j=0;j<m;j++){
if(W[i][j]==0)Q0[i][j]=INF;
else Q0[i][j]=W[i][j];
}
}
//Finding Shortest Path
for(k=0;k<m;k++){
for(i=0;i<m;i++){
for(j=0;j<m;j++){
Q0[i][j]=MIN(Q0[i][j],Q0[i][k]+Q0[k][j]);
}
}
}
//Printing Shortest Path
cout<<"Shortest Paths:"<<endl;
for(i=0;i<m;i++){
for(j=0;j<m;j++){
cout<<Q0[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
return 0;
}
Simulation Process to Find Shortest Path
Consider a given matrix W for a weighted graph:
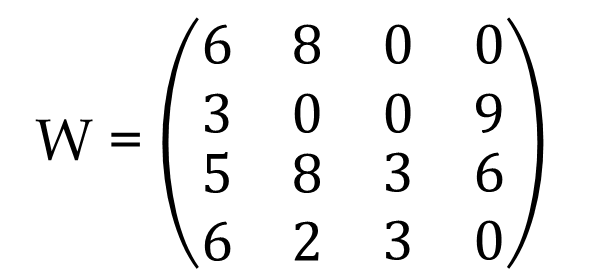
Mind it, we are searching for shortest path. But in the given graph 0 means there is no edge. If we try to find shortest path with this matrix 0 will be considered as shortest path. So we need to replace 0. Consider that there is a edge which is of infinity length, and for that you cannot reach. So replace the value 0 with Infinity. Infinity will be treated as the worst or longest way. So the algorithm will try to find a shortest path.
It is also important that if there is any infinity remaining in the matrix after simulating warshall algorithm you need to replace them with 0 again. This can be occur only in case of that graph which is not strongly connected. Although warshall algorithm ignores those graphs which are not strongly connected.
So, Derive Q0 :
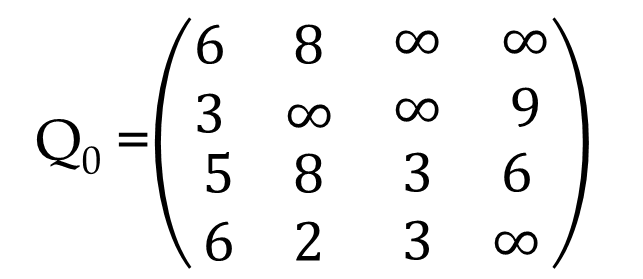
Derive Q1 using Warshall Algorithm. For easy check for any value in the container row and column and try to add n’th value of that column with n’th value of that row then check whether it is smaller than previous one. For example in the above matrix there is a infinity in 2nd row 2nd column. Add the first value of 2nd row and 2nd column and compare with current value. Hope you got 11. You can compare others also (i.e. third value of 2nd row and 2nd column or fourth value of 2nd row and 2nd column) The whole process will go through this. If the graph is strongly connected all infinity will be vanished after n’th step where n is the number of nodes in the graph.
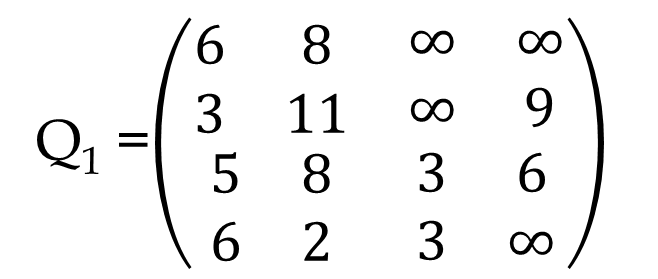
Derive Q2 in similar way:
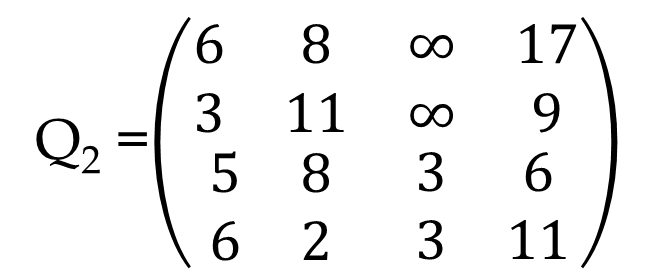
Derive Q3 :
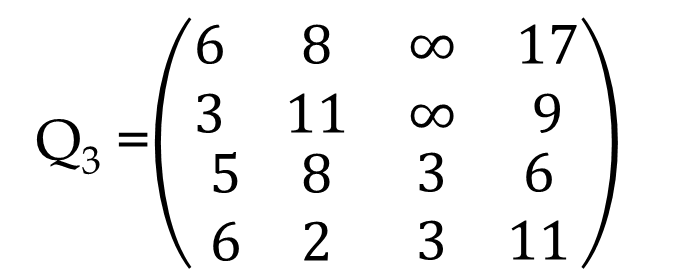
Derive Q4 :
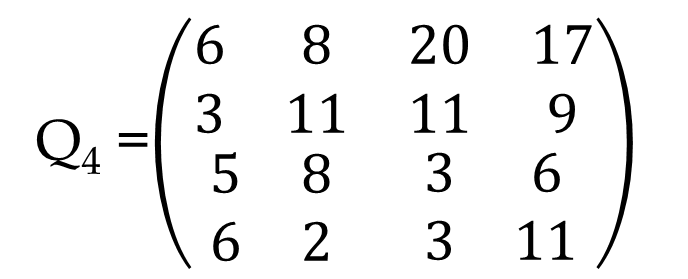
As we reach n’th step so the algorithm is complete.
Hope you like the tutorial. Comment what you feel. If you have any confusion comment to let me know. Subscribe for latest posts.
