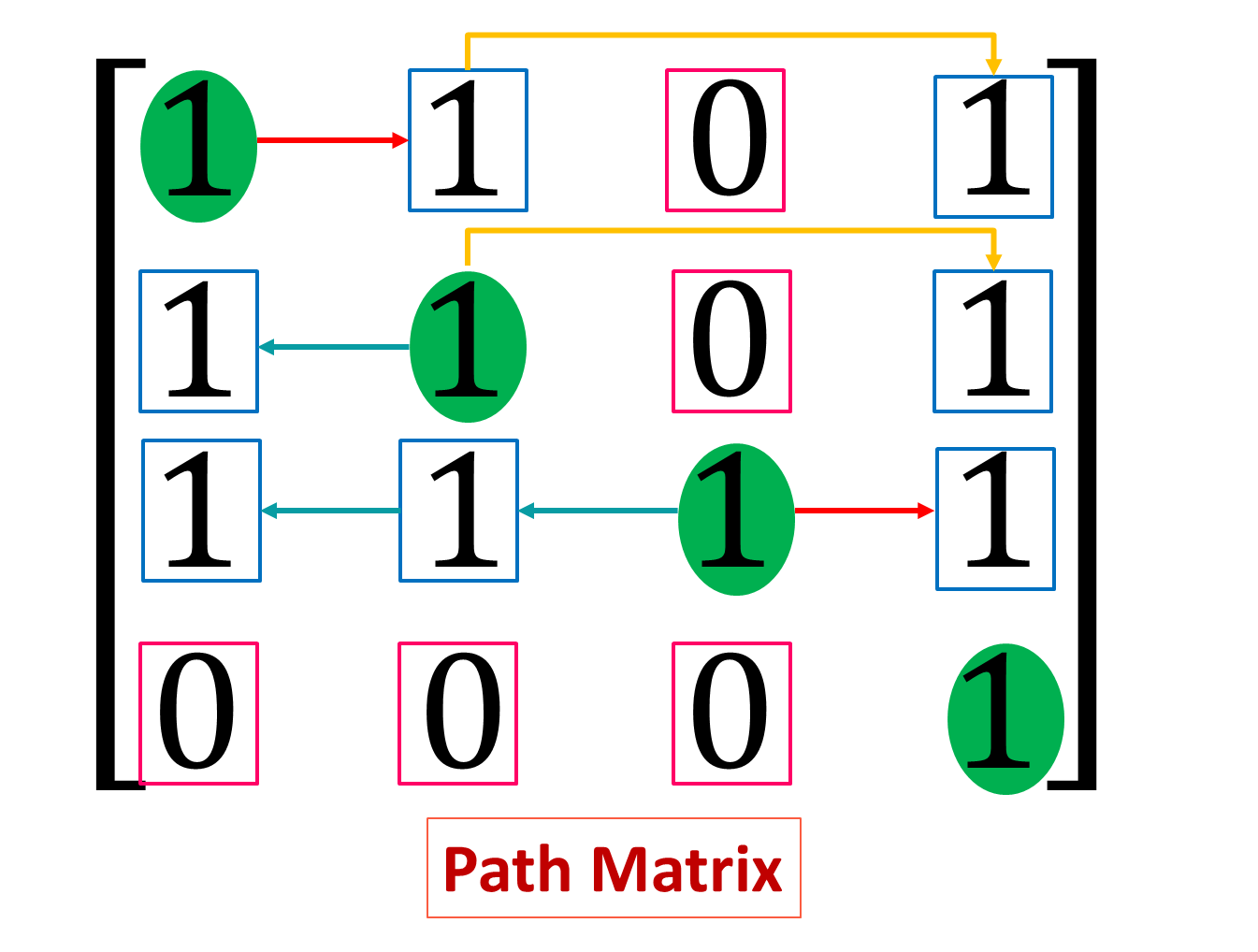
Path Matrix in Data Structure with Example
Path Matrix refers to a special type of data representation in data structure specially in graph theory. Path Matrix represents the availability of a path from a node to another node.
What is Path Matrix?
A path matrix is a matrix representing a graph, where each value in m’th row and n’th column project whether there is a path from node m to node n. The path may be direct or indirect. It may have a single edge or multiple edge.
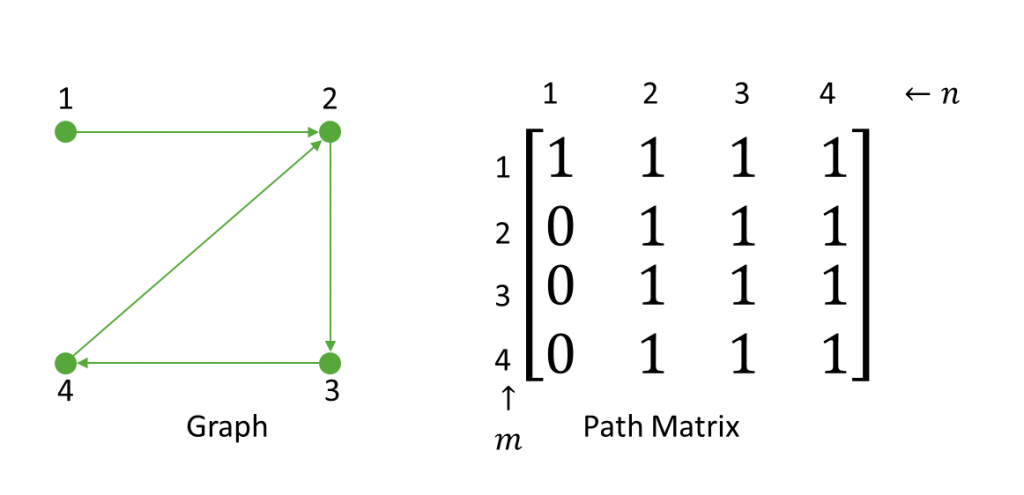
A path matrix defines whether there is a path between two nodes. So, in the above figure there is no direct path between:
- 1-3
- 1-4
- 2-4
- 3-2
But they have value 1 in the path matrix. Because, these path can be defined as,
- 1-2-3
- 1-2-3-4
- 2-3-4
- 3-4-2
So, these nodes can be traveled and the path matrix will have value 1 in corresponding cell.
Path Matrix in Data Structure
Graph Theory needs to use Path Matrix in Data Structure. Path Matrix is a special kind of data structure which is represented in matrix form. So, we discuss, calculate and manipulate path matrix in data structure.
Data Structure has a specific algorithm to calculate Path Matrix. The Algorithm is known as Warshall Algorithm.
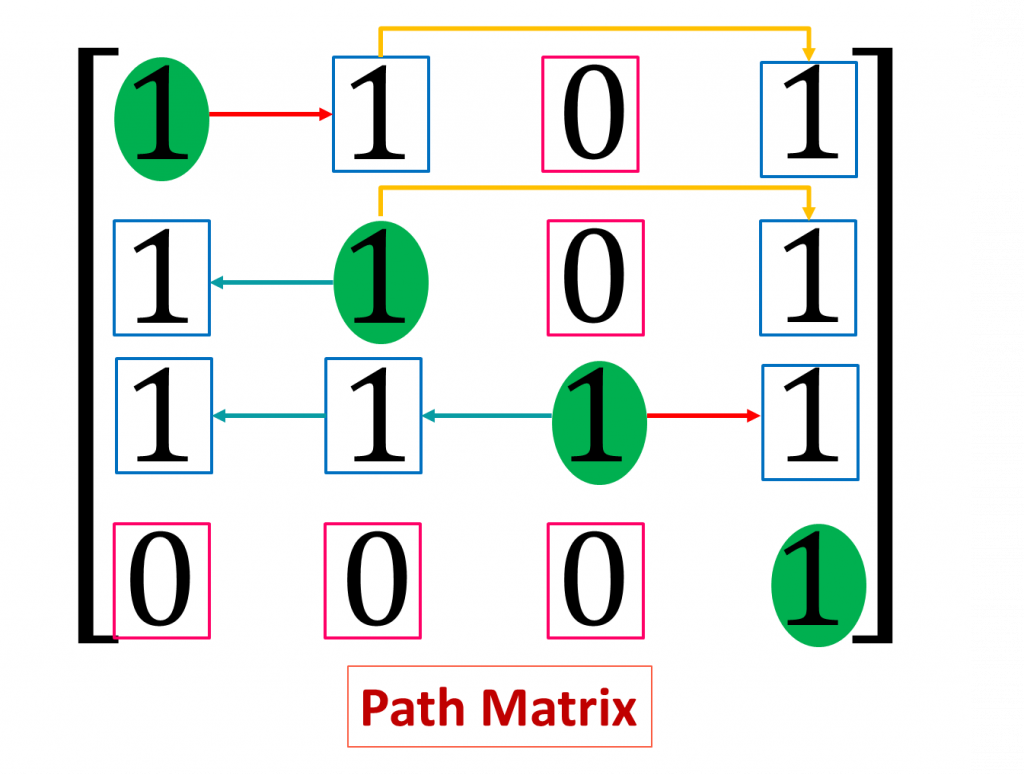
Path Matrix in Graph Theory
Graph Theory is dependent on vertex (node) and edge (path) relationship. So, each and every process needs path matrix in graph theory. To find a path between two vertex or node path matrix is the most easiest way. If you have a path matrix defined for a graph you can say whether a node can be traveled from another specific node.
Below is a real life Data Structure example of Path Matrix in Graph Theory.
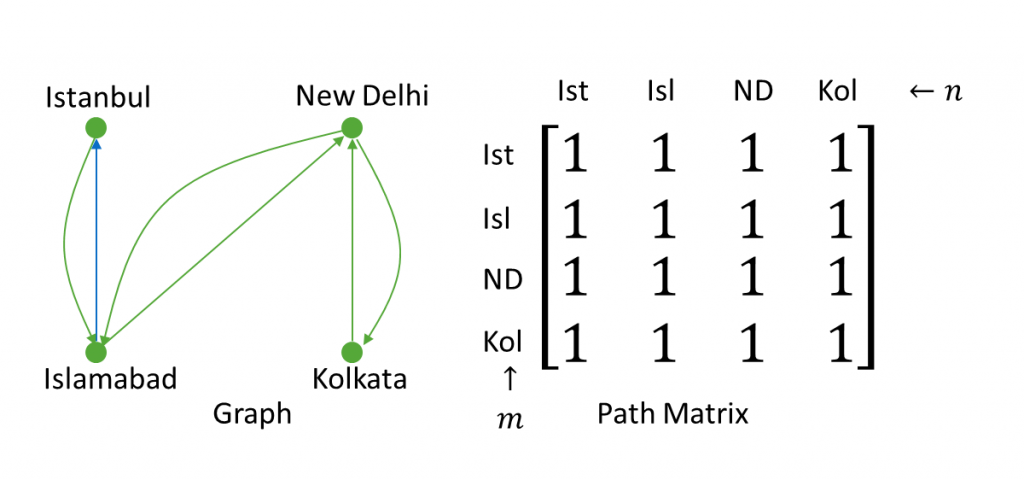
This graph defines train routes among India, Pakistan and Turkey. So, We can answer the following answer from the path matrix of the graph.
Is there a train route between New Delhi and Istanbul?
Ans: Yes.
Is there a train route between Kolkata and Istanbul?
Ans: Yes.
Is there a train route between Islamabad and Kolkata?
Ans: Yes.
And that is how path matrix works.
Where does Path Matrix used?
Path Matrix is used to define whether there is a available route between two place. Most of Mapping systems uses Path Matrix.
Example of Path Matrix
Here is another example of Path Matrix of a Graph. Also given C++ code and simulation process to calculate the Path Matrix.
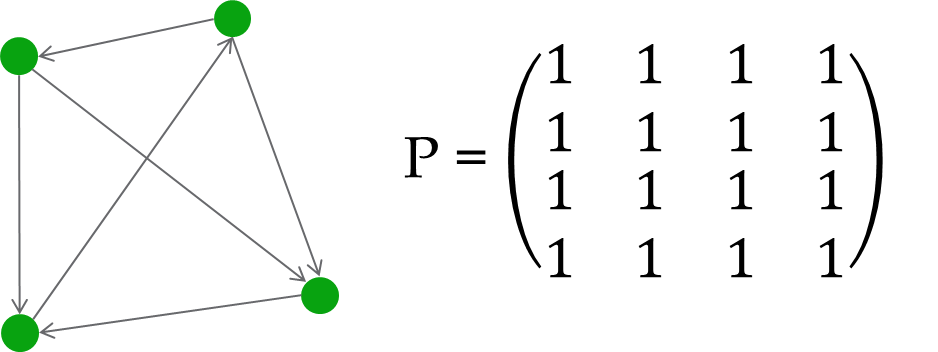
Find Path Matrix Using Warshall Algorithm in C++
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){ //Main Function
int m,i,j,k;
//m is Number of Vertices or Point
//i,j,k is normal integer to forward loop
cout<<"Number of Vertics will be: ";
cin>>m;
long A[m][m],P[m][m];
//A is name of Adjacency Matrix
//P is the name of Path Matrix
//For loop to take input the Adjacency Matrix
cout<<"Enter the Adjacency Matrix Below in "<<m<<"x"<<m<<" size:"<<endl;
for(i=0;i<m;i++){
for(j=0;j<m;j++){
cin>>A[i][j];
if(A[i][j]!=0)P[i][j]=1; //Finding path matrix
else P[i][j]=0;
}
}
cout<<endl;
//Finding Warshall's Path Matrix
for(i=0;i<m;i++){
for(j=0;j<m;j++){
for(k=0;k<m;k++){
P[i][j]=P[i][j]+P[i][k]*P[k][j];
if(P[i][j]!=0)P[i][j]=1;
}
}
}
//Printing Path Matrix
cout<<"Path Matrix :"<<endl;
for(i=0;i<m;i++){
for(j=0;j<m;j++){
cout<<P[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
return 0;
}
Highlighted part is the basic Warshall Algorithm.
Simulation Process to Find Path Matrix
Consider the graph:
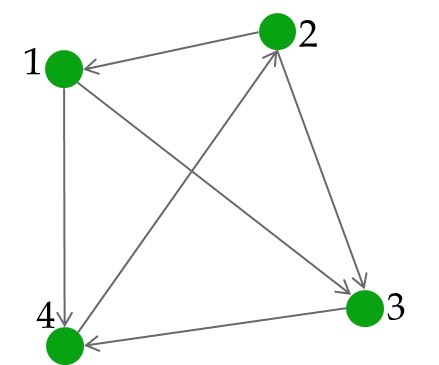
Adjacency Matrix for this graph is:
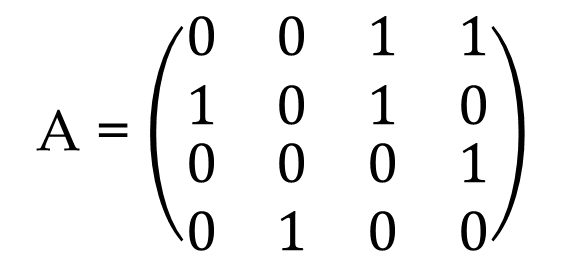
Derive A2 :
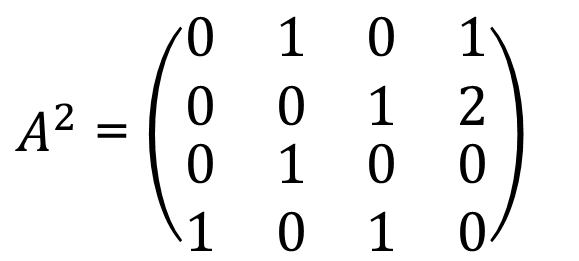
Derive A3 :
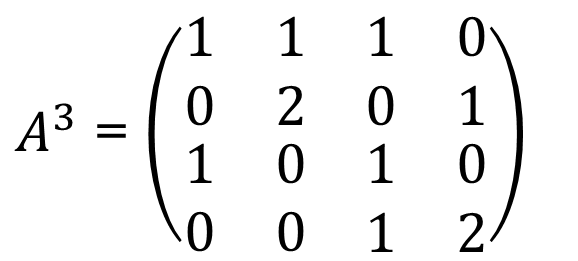
Derive A4 :

Sum up all four matrix to derive B4 :
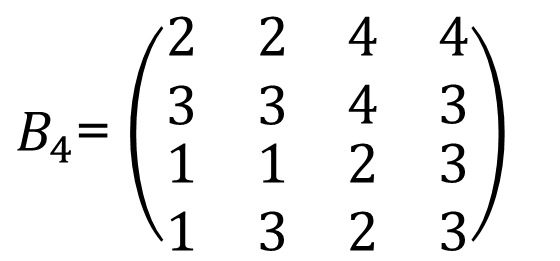
Derive Path Matrix P from B4 by replacing any none zero value with 1:
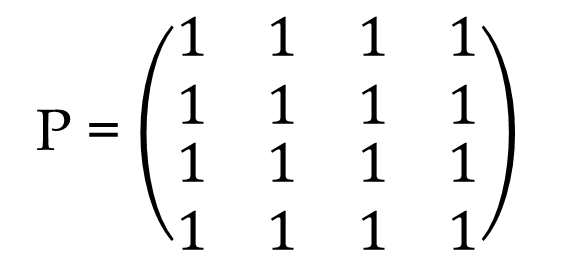
This is the path matrix. In Warshall Algorithm nothing but this is done using a loop.
Save Tutorial Bit in your Bookmark for Next Need. Thank You.
